Calculation Of Flywheel Effect GD²

• In case that a load is acquired through the connection of a gearhead, the motor shaft component of the load inertia should be calculated to select the motor.
• Also, the calculation method of GD² is different depending on the type of a load, and the following table provides GD² calculation method for each shape.

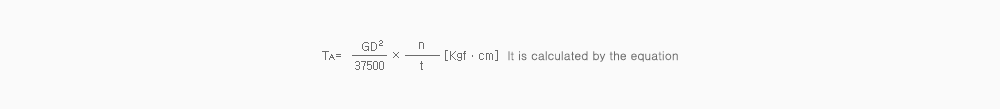
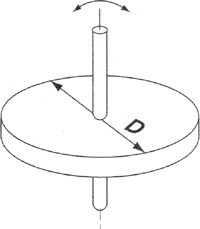
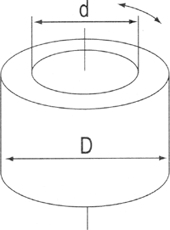
	Circulular Disk	Hollow
Shape
GD² Equation	W : Mass(kgf) D : Outer Diameter(㎝)	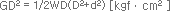W : Mass(kgf) D : Outer Diameter(㎝)

	Sphere	Hexahedron
Shape
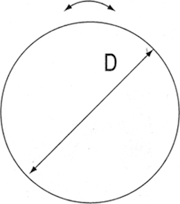
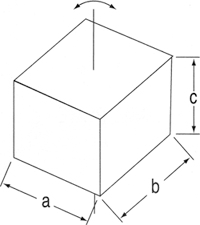
GD² Equation	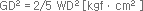W : Mass(kgf) D : Outer Diameter(㎝)	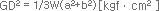W : Mass(kgf) a,b : Length of Side(㎝)

	POLE
Shape
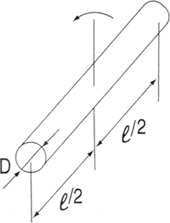
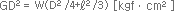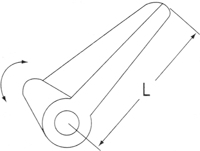
GD² Equation	W: : Mass(kgf) D : Outer Diameter(㎝) ℓ : Length(㎝)	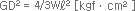W : Mass(kgf) ℓ : Length(㎝)

	Linear Motion (Horizontal)	Linear Motion (Vertical)
Shape
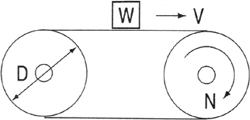
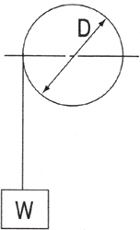
GD² Equation	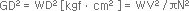V : Conveyor Speed (cm/min) N : Drum Rotational Speed (rpm) W : Weight Over Conveyor(kgf) D : Drum Outside Diameter (㎝) (Not included GD² for belt and drum)	GD² : WD² [kgf·㎠] W : Mass(kgf) D : Diameter(㎝)

	Gearhead	Operation of Ball Screw
Shape
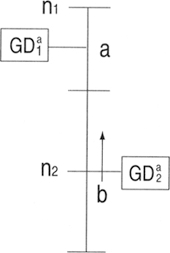
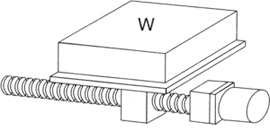
GD² Equation	a-axis component of tatal GD²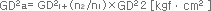 n₁ : Rotational speed of a-axis n₂ : Rotational speed pf b-axis Reduction ratio is n₁/n₂(i >1)	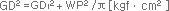GD²1 : Ball Screw GD² P : Pitch of Ball Screw(㎝) W : Total weight of table and work

	GD² of Arbitrary shaft
Shape
GD² Equation	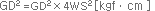D : Diameter (㎝), W : Mass (kgf), S : Radius of Rotation (㎝)

• When the brake motor is used, the inertia moment of a load has a greater impact on stop time, overrun, and stop precision. The relationship between the inertia moment J and the flywheel effect GD² expressed as the following equation.

Flywheel Effect
J : Inertia Moment

• When the deceleration is applied using a gearhead, the motor shaft component of GD² is represented by 1/(Gear Ratio)². The equation is as follows.

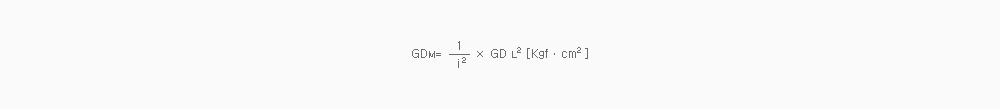
GDM : Motor Axis Component of GD²
GDL² : Assembled Load of GD² on Gearhead
i : Reduction Ratio of a Gearhead

• For example, if a gearhead with a ratio of 1/18 is used and the inertia of a load (GDL²) is 1000[kgf , cm²], the component of the motor shaft is

• If converted to Sl units of the inertia moment, the inertia moment is expressed as l in Sl units and this is represented as an equation below.

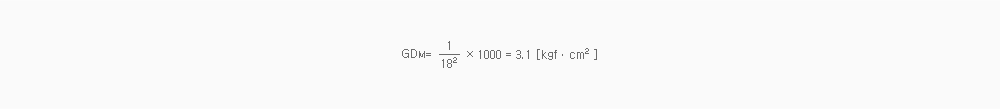
g : Gravitational Acceleration 9.80665 [m/sec²]

• Indicated allowable inertia load in below chart. Please use in less than value indicated.

EXPLICIT CALCULATION METHOD OF MOTOR CAPACITY

SIZE	Output	Allowable inertia load in the motor shaft
		GD²[kg.fcm]
□ 60	6W	0.25
□ 70	15W	0.57
□ 80	15W,25W	1.20
□ 90	40W	3.00
□ 90	60W	3.00
□ 90	90W,120W,150W	4.60
□ 90	80W,200W	6.00

• Allowable inertia load in the gearhead shaft is as below according to gear ratio.

Gear ratio 1/3~1/5

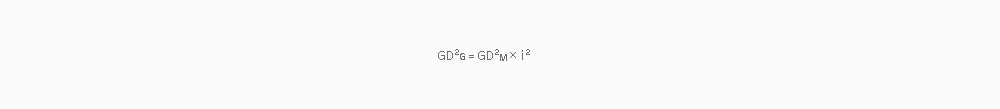
Gear ratio 1/60우

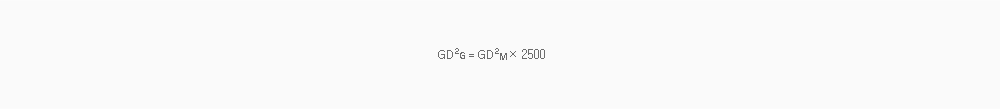
GD²G : Allowable inertia in gearhead shaft
GD²M : Allowable inertia in motor shaft
i : Gear ratio of Gear Head